§ 高斯投影坐标正反算公式
任何一种投影 ① 坐标对应关系是最主要的; ② 如果是正形投影,除了满足正形投影的条件外( C-R 偏微分方程),还有它本身的特殊条件。
1.1 高斯投影坐标正算公式: B,![]()
![]() x,y
x,y
高斯投影必须满足以下三个条件 :
① 中央子午线投影后为直线; ② 中央子午线投影后长度不变; ③ 投影具有正形性质,即正形投影条件。
由第一条件知中央子午线东西两侧的投影必然对称于中央子午线,即 (8-10) 式中, x 为 ![]() 的偶函数, y 为
的偶函数, y 为 ![]() 的奇函数;
的奇函数; ![]() ,即
,即 ![]() ,如展开为
,如展开为 ![]() 的级数,收敛。
的级数,收敛。
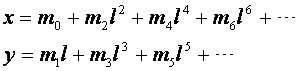 ( 8-33 )
( 8-33 )
式中 ![]() 是待定系数,它们都是纬度 B 的函数。
是待定系数,它们都是纬度 B 的函数。
由第三个条件知:
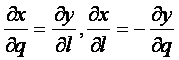
(8-33) 式分别对 ![]() 和 q 求偏导数并代入上式
和 q 求偏导数并代入上式
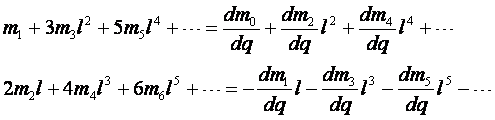 (8-34)
(8-34)
上两式两边相等,其必要充分条件是同次幂 ![]() 前的系数应相等,即
前的系数应相等,即
 (8-35)
(8-35)
(8-35) 是一种递推公式,只要确定了 ![]() 就可依次确定其余各系数。
就可依次确定其余各系数。 ![]()
由第二条件知 : 位于中央子午线上的点,投影后的纵坐标 x 应等于投影前从赤道量至该点的子午线弧长 X ,即 (8-33) 式第一式中,当 ![]() 时有:
时有:
![]() (8-36)
(8-36)
顾及 ( 对于中央子午线 )
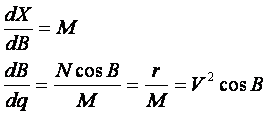
得:
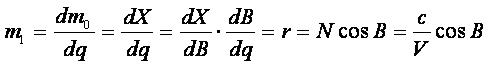 (8-37,38)
(8-37,38)
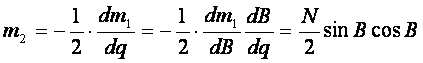 (8-39)
(8-39)
依次求得 ![]() 并代入 (8-33) 式,得到高斯投影正算公式
并代入 (8-33) 式,得到高斯投影正算公式
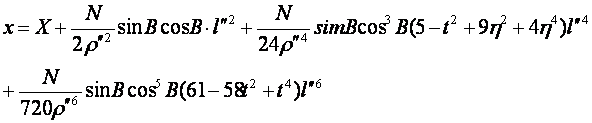
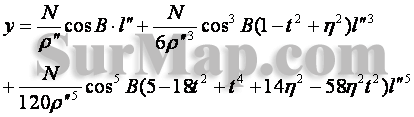 (8-42)
(8-42)
1.2 高斯投影坐标反算公式
x,y ![]() B,
B,![]()
投影方程:
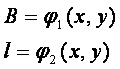 (8-43)
(8-43)
满足以下三个条件 :
①x 坐标轴投影后为中央子午线是投影的对称轴; ② x 坐标轴投影后长度不变; ③ 投影具有正形性质,即正形投影条件。
高斯投影坐标反算公式推导要复杂些。
① 由 x 求底点纬度 ( 垂足纬度 )![]() , 对应的有底点处的等量纬度
, 对应的有底点处的等量纬度 ![]() ,求 x,y 与
,求 x,y 与 ![]() 的关系式,仿照 (8-10) 式有,
的关系式,仿照 (8-10) 式有,
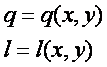
由于 y 和椭球半径相比较小 (1/16.37) ,可将 ![]() 展开为 y 的幂级数;又由于是对称投影, q 必是 y 的偶函数,
展开为 y 的幂级数;又由于是对称投影, q 必是 y 的偶函数, ![]() 必是 y 的奇函数。
必是 y 的奇函数。
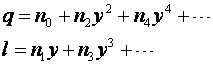 (8-45)
(8-45)
![]() 是待定系数,它们都是 x 的函数 .
是待定系数,它们都是 x 的函数 .
由第三条件知:
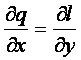 ,
,
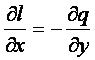 , (8-21)
, (8-21)
(8-45) 式分别对 x 和 y 求偏导数并代入上式
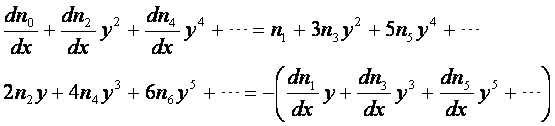
上式相等必要充分条件,是同次幂 y 前的系数相等,
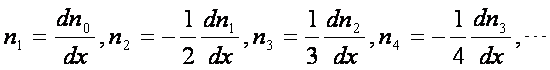
第二条件,当 y=0 时,点在中央子午线上,即 x=X ,对应的点称为底点,其纬度为底点纬度 ![]() ,也就是 x=X 时的子午线弧长所对应的纬度,设所对应的等量纬度为
,也就是 x=X 时的子午线弧长所对应的纬度,设所对应的等量纬度为 ![]() 。也就是在底点展开为 y 的幂级数。
。也就是在底点展开为 y 的幂级数。
由 (8-45)1 式
![]()
依次求得其它各系数
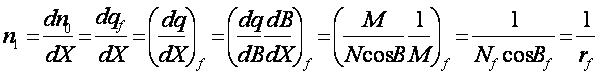
(8-51)
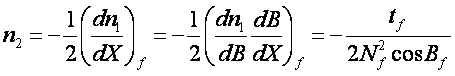 (8-51)1
(8-51)1
…………
将 ![]() 代入 (8-45)1 式得
代入 (8-45)1 式得
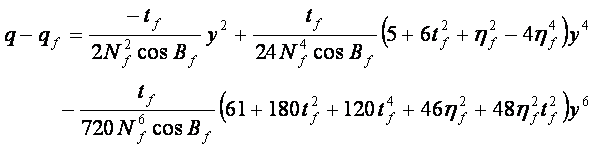
(8-55)1
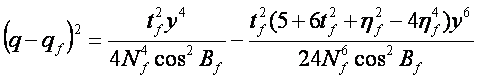
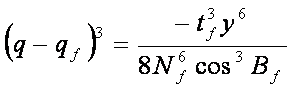 (8-55)
(8-55)
将 ![]() 代入 (8-45)2 式得 (8-56)2 式。 ( 最后表达式 )
代入 (8-45)2 式得 (8-56)2 式。 ( 最后表达式 )
② 求 ![]() 与
与 ![]() 的关系。
的关系。
由 (8-7) 式 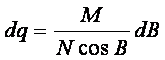 知:
知:
![]() (8-47)
(8-47)
![]() (8-48)
(8-48)
按台劳级数在 ![]() 展开
展开
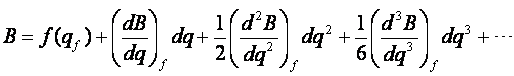 (8-49)
(8-49)
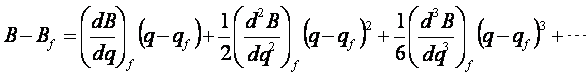 (8-50)
(8-50)
由 (8-7) 式可求出各阶导数:
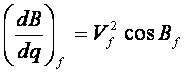 (8-53)
(8-53)
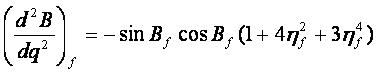 (8-54)1
(8-54)1
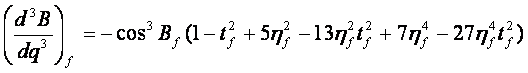 (8-54)2
(8-54)2
…………………
将式 (8-55)1,(8-55),(8-53),(8-54) 代入 (8-50) 式并按 y 幂集合得高斯投影坐标反算公式 (8-56)1,
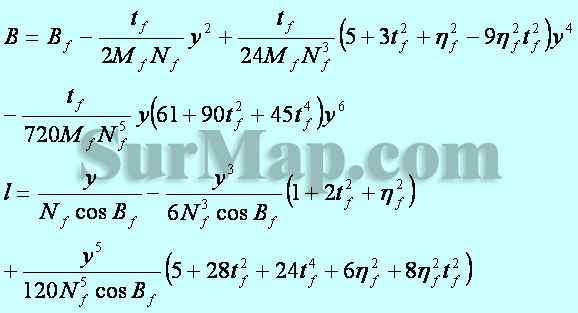 (8-56)
(8-56)
归纳由 ![]() 求
求 ![]() 的基本思想 :由点
的基本思想 :由点 ![]() 得到底点
得到底点 ![]() ,将底点 f 作为过渡,也就是说将坐标原点 o 移到 f 点,先求
,将底点 f 作为过渡,也就是说将坐标原点 o 移到 f 点,先求 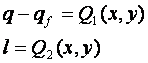 关系式,再将
关系式,再将 ![]() 关系式代入
关系式代入 ![]() 关系式得
关系式得 ![]() 关系式,最后将坐标原点移回到 o 点 , 从而求得
关系式,最后将坐标原点移回到 o 点 , 从而求得 ![]() 点。
点。
1.3 高斯投影坐标正反算公式的几何解释
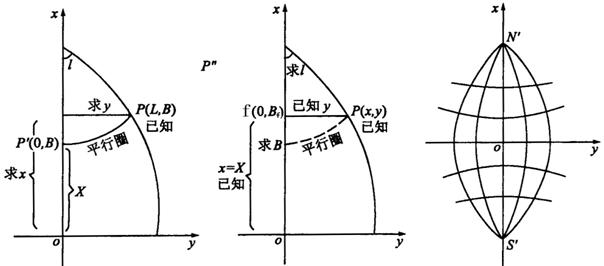
① 当 B=0 时 x=X=0 , y 则随 l 的变化而变化,这就是说,赤道投影为一直线且为 y 轴。当 l=0 时 , 则 y=0,x=X, 这就是说,中央子午线投影亦为直线,且为 x 轴,其长度与中央子午线长度相等。两轴的交点为坐标原点。 ② 当 l= 常数时 ( 经线 ), 随着 B 值增加, x 值增大, y 值减小,这就告诉我们,经线是凹向中央子午线的曲线,且收敛于两极。又因 ![]() ,即当用 -B 代替 B 时, y 值不变,而 x 值数值相等符号相反,这就说明赤道是投影的对称轴。 ③ 当 B= 常数时 ( 纬线 ) ,随着的 l 增加, x 值和 y 值都增大,这就是说,纬线是凸向赤道的曲线。又当用 -l 代替 l 时, x 值不变,而 y 值数值相等符号相反,这就说明,中央子午线是投影对称轴。由于满足正形投影条件,所以经线和纬线的投影是互相垂直的。 ④ 距中央子午线愈远的子午线,投影后弯曲愈厉害,表明长度变形愈大。
,即当用 -B 代替 B 时, y 值不变,而 x 值数值相等符号相反,这就说明赤道是投影的对称轴。 ③ 当 B= 常数时 ( 纬线 ) ,随着的 l 增加, x 值和 y 值都增大,这就是说,纬线是凸向赤道的曲线。又当用 -l 代替 l 时, x 值不变,而 y 值数值相等符号相反,这就说明,中央子午线是投影对称轴。由于满足正形投影条件,所以经线和纬线的投影是互相垂直的。 ④ 距中央子午线愈远的子午线,投影后弯曲愈厉害,表明长度变形愈大。